

With a length of 1,036 metres (3,399 ft), the Eupalinian subterranean aqueduct is famous today as one of the masterpieces of ancient engineering. The tunnel is the second known tunnel in history which was excavated from both ends. They did it to reduce the time to create the tunnel. In order to align the two tunnels, Eupalinos first constructed a "mountain line", running over the top of the mountain at the easiest part of the summit even though this gave a non-optimal position both for feeding water into the tunnel and for water delivery to the city. He connected a “south line” to the mountain line at the south side going straight into the mountain, which formed the south tunnel. At the north side a “north line” is connected to the mountain line, guiding the cut into the mountain from the north side. As the workers dug, they checked that their course remained straight by making sightings back towards the entrance of the tunnel. This is shown by a point in the southern half of the tunnel where the course accidentally diverged to the west and had to be corrected; a notch has been cut out of the rock on the inside of the curve, in order to restore the sight line. After 273 metres from the northern end, an area full of water, weak rock and mud forced Eupalinos to modify his plan and direct the tunnel to the west. When leaving the line Eupalinos planned his diversion as an isosceles triangle, with angles 22.5, 45, and 22.5 degrees. Measuring errors occurred and Eupalinos slightly overshot. When this was realised, the north tunnel was redirected to the east once more. The cutting of the south tunnel was completely straight, but stopped after 390 metres (1,280 ft).
The north and south halves of the tunnel meet in the middle of the mountain at a dog-leg, a technique to assure they did not miss each other. In planning the dig, Eupalinos used now well-known principles of geometry, codified by Euclid several centuries later. Errors in measurement and staking could cause Eupalinos to miss the meeting point of the two teams, either horizontally or vertically. He therefore employed the following techniques.
Eupalinos calculated the expected position of the meeting point in the mountain. Since two parallel lines never meet, an error of more than two metres horizontally meant that the north and south tunnels would never meet. Therefore, Eupalinos changed the direction of both tunnels. This gave a catching width that was wider by 17 metres (56 ft), so that a crossing point would be guaranteed, even if the tunnels were previously parallel and far away. They thus meet at nearly a right angle.
At the start of work, Eupalinos levelled around the mountain probably following a contour line in order to ensure that both tunnels were started at the same altitude. The possibility of vertical deviations in the process of excavation remained, however. He increased the possibility of the two tunnels meeting each other, by increasing the height of both tunnels at the point near the join. In the north tunnel he kept the floor horizontal and increased the height of the roof by 2.5 metres, while in the south tunnel he kept the roof horizontal and lowered the level of the floor by 0.6 metres. His precautions as to vertical deviation proved unnecessary, however, since measurements show that there was very little error. At the rendezvous, the closing error in altitude for the two tunnels was a few millimetres.
![]() | | Öffentlich
| | Öffentlich

Wählen Sie eine der beliebtesten Aktivitäten unten aus oder verfeinern Sie Ihre Suche.
Entdecken Sie die schönsten und beliebtesten Routen in der Gegend, sorgfältig gebündelt in einer passenden Auswahl.
Datenquelle: Zach Marchall (CC BY-SA 2.0)
Wählen Sie eine der unten aufgeführten beliebtesten Kategorien oder lassen Sie sich von unserer Auswahl inspirieren.
Entdecken Sie die schönsten und beliebtesten Sehenswürdigkeiten der Gegend, sorgfältig gebündelt in einer entsprechenden Auswahl.
Datenquelle: Zach Marchall (CC BY-SA 2.0)
Mit RouteYou kannst du ganz einfach eigene Karten erstellen. Plane deine Route, füge Wegpunkte oder Knotenpunkte hinzu, plane Sehenswürdigkeiten und Einkehrmöglichkeiten ein und teile alles mit Familie und Freunden.
Routenplaner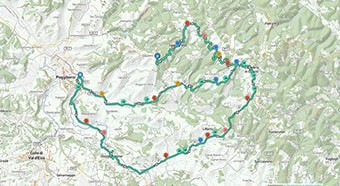
<iframe src="https://plugin.routeyou.com/poiviewer/free/?language=de&params.poi.id=8277791&params.language=en" width="100%" height="600" frameborder="0" allowfullscreen></iframe>
© 2006-2026 RouteYou - www.routeyou.com